Logaritma adalah operasi matematika yang merupakan invers (kebalikan) dari eksponen atau pemangkatan.
Atau dengan pengertian lain, bentuk eksponen bila dinyatakan dengan notasi logaritma adalah
bila dinyatakan dengan notasi logaritma adalah  .
.
dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan sama artinya dengan
sama artinya dengan  .
.
Atau dengan pengertian lain, bentuk eksponen
 bila dinyatakan dengan notasi logaritma adalah
bila dinyatakan dengan notasi logaritma adalah  .
.dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan
 sama artinya dengan
sama artinya dengan  .
.
B. Sifat – sifat Logaritma
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :

Contoh Soal :
1. Diketahui dan
dan 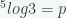 . Nilai
. Nilai  dinyatakan dalam p dan q adalah … (UN SMA 2013)
dinyatakan dalam p dan q adalah … (UN SMA 2013)
1. Diketahui
Penyelesaian :

2. Hasil dari  adalah … (UN SMA 2012)
adalah … (UN SMA 2012)
 adalah … (UN SMA 2012)
adalah … (UN SMA 2012)
Penyelesaian :

3. 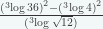 = … (Sipenmaru 1987)
= … (Sipenmaru 1987)
Penyelesaian :
Ingat sifat aljabar


Maka gunakan sifat tersebut untuk menyelesaikan pembilangnya.
Jadi,

Jadi,

4.  sama dengan … (SPMB 2012)
sama dengan … (SPMB 2012)
Penyelesaian :

5. 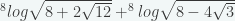 sama dengan …
sama dengan …
Penyelesaian :
Ingat bahwa :


Maka persamaan dapat disederhanakan menjadi :


6. Jika  , maka
, maka 
sama dengan … (UMPTN 2005)
sama dengan … (UMPTN 2005)
Penyelesaian :


Cara Cepat :
Bentuk  akan terdefinisi jika
akan terdefinisi jika  . Maka substitusikan sembarang x anggota ℝ kecuali
. Maka substitusikan sembarang x anggota ℝ kecuali 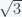 .
.
 akan terdefinisi jika
akan terdefinisi jika  . Maka substitusikan sembarang x anggota ℝ kecuali
. Maka substitusikan sembarang x anggota ℝ kecuali
Misal x = 3, maka f(3) + f(1) = -1 + 0 = -1.
7. Jika  , maka
, maka 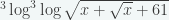 = …
= …
Penyelesaian :


Maka,


8. Jika x memenuhi persamaan  , maka
, maka  = …
= …
Penyelesaian :

Jadi,


9. Nilai x yang memenuhi  adalah … (UMPTN 2000)
adalah … (UMPTN 2000)
Penyelesaian :

10. Jika 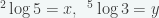 , maka nilai
, maka nilai 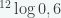 dalam x dan y adalah …
dalam x dan y adalah …
Penyelesaian :

11. Jika 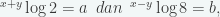 dengan x>y>0 maka
dengan x>y>0 maka 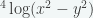 = … (UM UGM 2010)
= … (UM UGM 2010)
Penyelesaian :

Dari persamaan (1) dan (2) di dapat :
12. What is the value of the expression
Penyelesaian :
Ingat bahwa  adalah bentuk lain dari
adalah bentuk lain dari 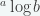 dan
dan 
Note : 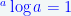
Jadi,
Semoga bermanfaat 

Komentar
Posting Komentar